“斐波那契数列(Fibonacci)”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年,籍贯大概是比萨)。他被人称作“比萨的列昂纳多”。斐波那契数列是一个古老而有趣的问题,由于其所具有的各种特殊属性,它与最优美的黄金分割有这密不可分的关系。在数学领域以及自然界中随处可见,而且正逐渐被应用在人们的日常生活与娱乐中。
斐波那契数列又称“斐波那契神奇数列”,是由13世纪的意大利数学家斐波那契提出的,当时是和兔子的繁殖问题有关的,它是一个很重要的数学模型。假设一对成年兔子放于围栏中,每月可生下一对一雌一雄的小兔,而小兔出生一个月后便可以生育小兔,且每月都生下一对一雌一雄的小兔.问把这样一对初生的小兔置于围栏中,一年后围栏中共有多少对兔子(假定兔子没有死亡)?据此,可得月份与兔子对数之间的对应关系如下:

满足(1)式的数列就叫做斐波那契数列,这是一个带有初值的用递推关系表示的数列。这个数列一问世就吸引了无数数学家的兴趣,以下是费氏数列的定义及通项公式。
费氏数列是是由一连串的数字所组成的(1、1、2、3、5、8、13、…),而且这串数字之间具有一定的规则,就是每一个数字必须是前两个数字的和( an =an-1 + an-2 )。
通项公式为: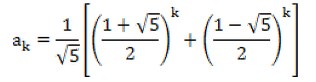
它的通项公式又叫“比内公式”,是用无理数表示有理数的一个范例。值得一提的是,斐波那契数列有许多重要而有趣的应用。例如,优选法中的分数法正是基于此数列;大自然中植物的叶序、菠萝中的鳞状花萼、蜜蜂进蜂房的方式数、艺术上的黄金分割点等都与斐波那契数列有着密切的联系。
黄金分割与费布纳西数列的关系
相邻两个菲波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。即f(n)/f(n- 1)-→0.618„。由于斐波那契数都是整数,两个整数相除之商是有理数,所以只是逐渐逼近黄金分割比这个无理数。但是当我们继续计算出后面更大的斐波那契数时,就会发现相邻两数之比确实是非常接近黄金分割比。
由递推关系式表示数量关系的Fibonacci 数列在以前并没有引起多大重视和震动,随着电子计算机的广泛应用,Fibonacci 数列这个古老的数学问题越来越受到人们的重视。费氏数列的多项性质运用在生活中一定能带来很多方便之处。费氏数列的前后项的比是黄金比例,这样的特性就可以再生活中需要用到黄金比的地方却又很难测出准确值时使用。另外的一些特性也都在数学、几何、美学甚至生物和营建都有很多的应用空间。




