人类曾经拥有一把刀;
它重量不如匕首,锋利胜过屠龙;
它貌似轻如鸿毛,出手横扫千均。
它纵横于哲学、物理、经济、语言学、管理学等领域;
迷惑了哲学家,激励了科学家,引领着企业家;
自14世纪横空出世后,它终结了繁琐复杂的学院争论;斩杀了卡尔·萨根的恐怖火龙。

14世纪时,欧洲学者忙于“口遁”,把研究“似是而非”的东西当作智慧象征。
例如:
黑色的白伞是否存在?
上帝的喷嚏还是哈欠导致了电闪雷鸣?
不是张三、也不是李四的人本身是否存在?
这些问题与中国的“白马非马,楚人非人”的诡辩学说,与“不是风动也不是幡动而是心动”此类无法证伪的观点有异曲同工之妙。
来自英格兰奥卡姆的逻辑学家威廉对此极其厌烦,这些学者争来争去全无实据,那口沫横飞的星子时常喷到威廉的脸上。
如果不是作为一个有教养的修士,他会直接说“你丫闭嘴”,最后他压制住满腔怒火,文诌诌地道:如无必要,勿增实体。
非常简单八个字,道出了事物本质。
通俗一点的解释:
如果能用A来描述现象,那么不要发明B来解释,新逻辑可能有漏洞。
延伸一点的理论:
如果同一个现象有n种理论,最简单的那个便是最正确的。
他再进一步提出一条实践原理:
能用n做好事情,那就不要有第n+1个动作。
这一把小小的剃刀,貌似简单,它却在不同学科中展现出巨大威力。
逻辑学应用:
斩杀“喷火的龙”
首先它斩杀了卡尔·萨根车库里的那条喷火的巨龙,让逻辑回归到正常状态。
“我的车库里有一条喷火的巨龙。”卡尔·萨根说。
卡尔的朋友问:“在哪里,我看看。”
“这条龙是隐形的,是看不见的。”卡尔·萨根故作高深。
“那真可惜,”朋友道,“让我摸摸它的逆鳞。”
“隐形的龙,不是想摸就能摸到的。”
朋友想了一下,“让它来喷我吧,我愿意测测火焰温度。”
“这条龙喷出的火是没有温度的,那是无形的温度。”
“那在地上撒上石灰,记录下龙的抓印。”
“这条龙是浮在空中的,不会在地上留下印痕。”卡尔又道。
“那,”朋友犹豫了一下,“总归有一种方法才观察到这条龙吧?”
卡尔·萨根道:“不,你提出任何一种观察方法,龙都有相应特性来避免观察。”
那么问题就来了,一条看不见摸不着,喷着没有热量的火,浮在空中不会留下足迹,用任何一种方法都观察不到的龙,同根本就没有龙,有什么区别呢?
这就是奥卡姆剃刀的标准应用:卡尔·萨根是个骗子,他的车库里根本就没有龙。
科学应用: 最小作用量原理 宇宙所有的规律,都要服从一些基本原理,如简单、对称、守恒、稳定。 还有一个很重要的原理:最小作用量原理(principle of least action)。
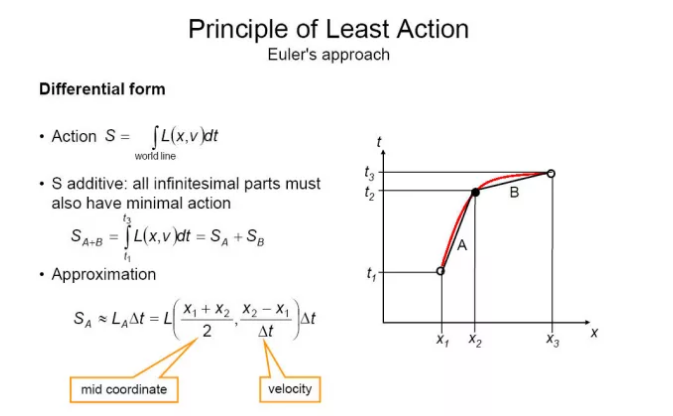
作用量S是拉格朗日函数的时间积分,含义很广,包括时间、空间、能量、概率。
作用量最小,意味着数学上的极小值、导数为零。
自由落体为什么会沿直线下落?光为什么沿直线传播?因为在近似平直的三维时空中,直线运动消耗的空间和时间作用量最小;在非平直的时空中,如球面,物体会沿着最短圆弧(测地线)运动;无重力环境下,物体会收缩成球形,因为体积不变时,收缩成球面积最小。
狗叼飞盘,走的是直线,因为时空消耗最短;而狼捕捉猎物,走的是弯曲路线,它要的是捕获概率最大(失败率最小),概率超过时空成为第一作用量。
经济学应用:
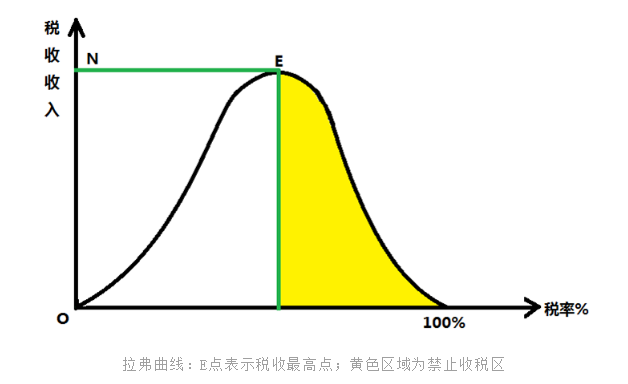
税收中的“拉弗曲线”
在经济系统中,税收是关键性控制手段之一。
那到底该如何调整税收呢,这是执政官们最烦恼的问题。
当年司马光和王安石在这个问题争执了一辈子,好友最终成为仇敌。
假设植物学家A和B争论西红柿是水果还是蔬菜,如果是水果则面临高税,而蔬菜由于是基本消费品则征低税或不征税。僵持不下,决策者C如何选择?
答案是,既然西红柿的生物学身份争议不清,那么就按照法律管制是必要的恶的原则,把西红柿当成蔬菜不征税。因为征收行为本身需要人力物力,很可能消耗的资源会超过征收带来的好处。
这把刀,你应该时常握在手里面。
因为它是真相之刃,帮你理清这“剪不断,理还乱”的世界。手持这把刀的人,既清醒,又智慧。
可惜的是,人类大多数已经迷失,在这复杂的世界、荒谬的骗局中忙乱奔走,慢慢地,已经忘记了这把最锋利的思想之刀。
当年,人类获得这把刀并不容易,剃刀主人威廉被视为异端,教会驱逐,帝国流放;死后经过笛卡儿、牛顿等大科哲加持后,历经百年,才磨成这闪闪发亮的理性刀片。
倘若这位14世纪的修士知道他的武器被人类遗忘,除了感慨一生流离外,会更加绝望于这个世界。 记住,这是真相之刃,锋利无敌。有骗局袭来时,拿起这把刀。它是骗子最害怕的武器。世界越来越复杂时,也祭起这把刀。看清楚世界的真相。




